Matlab Toolbox for the Analytical Diffusion/Helmholtz Solutions of a Sphere
The "Sphere-Diffusion" toolbox solves for the analytical solutions for the diffusion inside and outside a sphere. This toolbox is part of an open-source software, MMC, developed by Qianqian Fang. The license of the toolbox is GNU General Public License version 3. Please see LICENSE.txt for details.
The solutions are defined in the 3D space on a user specified grid; the sphere can have different absorption/scattering/refractive index to the background media. This toolbox can be useful when evaluating new algorithms in the heterogeneous media. The toolbox is compatible with GNU Octave.
- 1. Download
- 2. Core functions
- 3. Contour plots of the sample solutions
- 5. Comments on semi-infinite solutions
- 6. Examples
- 7. Acknowledgement
- 8. Reference
1. Download
Please browse the registration page to proceed with downloading.The author of the toolbox is appreciated if you can cite the references, [Fang2010] and [Boas1994], listed at the end of this document if you choose to use this toolbox in your publication.
2. Core functions
- [res,xi,yi,zi] = sphdiffusioninfinite(xrange,yrange,zrange,cfg)
- diffusion solution for a sphere inside the infinite homogeneous medium
- [res,xi,yi,zi] = sphdiffusionsemi(Reff,xrange,yrange,zrange,cfg)
- diffusion solution for a sphere inside a semi-infinite homogeneous medium
- [res,xi,yi,zi] = sphdiffusionslab(Reff1,Reff2,h,xrange,yrange,zrange,cfg)
- diffusion solution for a sphere inside an infinite homogeneous slab
3. Contour plots of the sample solutions
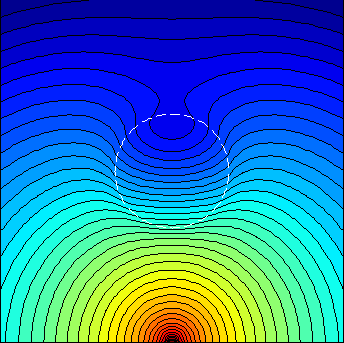
3.1.1. A 10mm sphere inside an infinite homogeneous medium
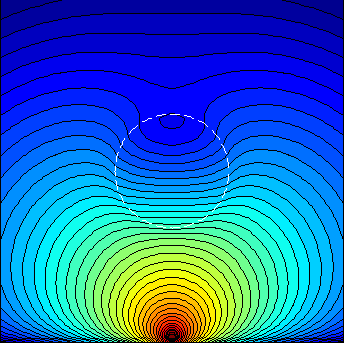
3.1.2. A 10mm sphere inside a semi-infinite homogeneous medium
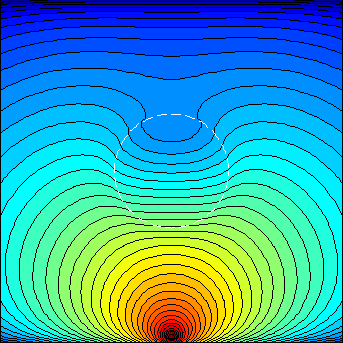
3.1.3. A 10mm sphere inside an infinite homogeneous slab
4. Other functions
| function | description |
|---|---|
| besselhprime.m | Hankel function first order derivative |
| besseljprime.m | Bessel function (Bessel first kind) first order derivative |
| besselyprime.m | Neumann function (Bessel second kind) first order derivative |
| spbesselh.m | Spherical Hankel function |
| spbesselhprime.m | Spherical Hankel function first order derivative |
| spbesselj.m | Spherical Bessel function |
| spbesseljprime.m | Spherical Bessel function first order derivative |
| spbessely.m | Spherical Neumann function |
| spbesselyprime.m | Spherical Neumann function first order derivative |
| spharmonic.m | Spherical harmonics |
| sphdiffAcoeff.m | Sphere exterior field coefficients |
| sphdiffBcoeff.m | Sphere exterior field coefficients |
| sphdiffCcoeff.m | Sphere interior field coefficient |
| sphdiffexterior.m | Sphere exterior total field |
| sphdiffincident.m | Incident field |
| sphdiffinterior.m | Sphere interior field |
| sphdiffscatter.m | Sphere exterior scattered field |
5. Comments on semi-infinite solutions
see the comments in the sphdiffusionsemi.m script
% high order terms are ignored, for example, the Phi(S2,O2) scattered by % real sphere O1, or Phi(S1,O1) scatted by the mirrored sphere O2 etc % % 1st order approximation works only when the sphere is far away from % source and interface so that multiple-scattering is weak. % % ____ % .' `. real sphere % / O1 \ % | o----|-----> x % \ | a / phi_interior=phi_interior(S1,O1) % `.__|_.' +phi_interior(S2,O1) % | phi_ext=phi_incident(S1,O1)+phi_scatter(S1,O1) % | - phi_incident(S2,O2)-phi_scatter(S2,O2) % | + phi_scatter(S1,O2) -phi_scatter(S2,O2) % | + high order terms(phi_scatter(S1,O1,O2),..) % S1 x real source % _______________________|____________________z0______ true boundary % | zb % -----------------------|---------------------- extrapolated boundary % ^ | zb % | | z0 % | S2 x mirrored source --- S2=-S1 % | | % | src0(1) | % | | % | ..|. mirrored sphere % | .' | `. % v / | a \ (origin for the mirrored field) % ------- : o----:-----> x % \ O2 / % `......' % %
6. Examples
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % setting up problem domain %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% cfg.v=299792458000; % speed-of-light in mm/s cfg.a=10; % radius of the sphere, mm cfg.omua=0.002; % outside (background) mua 1/mm cfg.omusp=0.990; % outside (background) mus' 1/mm cfg.imua=0.050; % inside (sphere) mua 1/mm cfg.imusp=0.500; % inside (sphere) mus' 1/mm %cfg.imua=0.002; %cfg.imusp=0.990; cfg.src=[30,pi,0]; % source position in spherical coordinates cfg.maxl=20; % maximum orders for the series expansion cfg.omega=0; % modulation frequency
cfg.Din=cfg.v/(3*cfg.imusp); % Diffusion coefficient in the sphere cfg.Dout=cfg.v/(3*cfg.omusp); % Diffusion coefficient outside the sphere cfg.kin=sqrt((-cfg.v*cfg.imua+i*cfg.omega)/cfg.Din); % complex-wavenumber in the sphere cfg.kout=sqrt((-cfg.v*cfg.omua+i*cfg.omega)/cfg.Dout); % complex-wavenumber outside the sphere
% solution of the sphere in an infinite medium [phi_ana,xa,ya,za]=sphdiffusioninfinite(-30:0.8:30,0,-30:0.8:30,cfg); figure;contourf(xa,za,log10(abs(phi_ana)),40);axis equal;
% solution of the sphere in an infinite slab with a height of 60mm [phi_ana,xa,ya,za]=sphdiffusionslab(0,0,60,-30:0.8:30,0,-30:0.8:30,cfg); figure;contourf(xa,za,log10(abs(phi_ana)),40);axis equal;
7. Acknowledgement
Qianqian Fang would like to thank David Boas for the helpful discussions on the semi-infinite solutions.
8. Reference
- Q. Fang, "Mesh-based Monte Carlo method using fast ray-tracing in Plücker coordinates," Biomed. Opt. Express 1, 165-175 (2010)
- D. A. Boas, M. A. O’Leary, B. Chance, and A. G. Yodh, “Scattering of diffuse photon density waves by spherical inhomogeneities within turbid media: analytic solution and applications,” Proc. Natl. Acad. Sci. U.S.A. 91(11), 4887–4891 (1994).
![[Home]](/img/mcx_wiki_banner.png)